- Home
- Microsoft 365
- Excel
- Reverse Calculate Weighted Average Scores
Reverse Calculate Weighted Average Scores
- Subscribe to RSS Feed
- Mark Discussion as New
- Mark Discussion as Read
- Pin this Discussion for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 15 2023 02:42 AM
I'm trying to reverse calculate the average for year 2024 I want to be 3.75 of 9 concepts weighted differently. More of a maths question I suppose but the formula would help as well as mathematical formula. Each weighing has a maximum score of 4. Please advise.
| Concept | Weighed | 2022 | 2023 | 2024 |
1 | 10% | 3.75 | 3.92 | |
2 | 10% | 2.82 | 3.76 | |
3 | 10% | 3.33 | 3.24 | |
4 | 12% | 3.35 | 3.5 | |
5 | 11% | 3.46 | 3.49 | |
6 | 10% | 3.7 | 3.75 | |
7 | 18% | 3.71 | 3.71 | |
8 | 15% | 2.93 | 3.71 | |
9 | 4% | 4 | 3.93 | |
| Average | 100% | 3.41 | 3.58 | 3.75 |
- Labels:
-
Excel
-
Formulas and Functions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 15 2023 04:34 AM
There are infinitely many solutions.
An easy one: 37.5 for concept 1, and 0 for concepts 2 to 9.
Another one: 3.75 for concepts 1 to 9.
Etc. etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 16 2023 12:45 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 16 2023 02:00 PM
How do you define minimum score?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 17 2023 04:50 AM
For example concept 7 in 2023 is weighed at 18% with a score of 3.71
And concept 8 in 2023 in 2023 is weighed at 15% with a score of 3.71
Because they're weighed differently they're not the same scores
If they were all weighted the same it would be a more simple solution of
Adding together the sum of each concept score divided by number of concepts.
However, they're not all weighted the same and this is my issue
For the desired 2024 trying to reverse calculate, I've tried
3.75 / 100% = .0375 (1%)
But if I were to x 10 = .375 (10%)
It doesn't add up unless for some reason I need to move the decimal point
To 3.75 which would then make sense but not sure why
Please advise
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 17 2023 05:32 AM
First, the calculated average for 2023 ist NOT 3.58 but 3.6524.
So I calculate the change from 2023 to 2024: 3.75/3.65 = 1.02672216.
And then multiply each value from 2023 with the change factor.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 17 2023 05:33 AM - edited Dec 17 2023 02:51 PM
You haven't explained yet what exactly you want to minimize.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 17 2023 06:25 AM
Writing Excel formulas using the LET function helps to make the calculations clearer. It requires Excel version 2021 or later.
See the attached workbook. Be sure to read the notes on the _Info worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 17 2023 06:33 AM
But the weighted average of your result is 1.84, not 3.75
If you want to minimize the sum of the amounts while keeping the weighted average to 3.75, you have to assign the max value of 4 to the rows with the highest percentages until you cannot do that anymore, then fit the amount for the next lower (or equal) percentage to arrive at 3.75.
| Concept | Weighed | 2022 | 2023 | 2024 |
| 1 | 10% | 3.75 | 3.92 | 4 |
| 2 | 10% | 2.82 | 3.76 | 4 |
| 3 | 10% | 3.33 | 3.24 | 4 |
| 4 | 12% | 3.35 | 3.5 | 4 |
| 5 | 11% | 3.46 | 3.49 | 4 |
| 6 | 10% | 3.7 | 3.75 | 3.1 |
| 7 | 18% | 3.71 | 3.71 | 4 |
| 8 | 15% | 2.93 | 3.71 | 4 |
| 9 | 4% | 4 | 3.93 | 0 |
| Average | 100% | 3.41 | 3.58 | 3.75 |
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 17 2023 06:41 AM
@Hans Vogelaar Cell F11 contains the target (read the formulas), not the weighted average of the cells above it. That usage makes the formulas reusable for other targets. As indicated in the formulas, and as you also write explicitly, all other concepts must have a value of 4 for these minimums to work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 17 2023 07:32 AM
If that is correct, I have completely misunderstood the question. It's not unusual...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 17 2023 01:53 PM
Concept Weighed 2022 2023 2024
1 10% 3.75 3.92 3.92
2 10% 2.82 3.76 3.9
3 10% 3.33 3.24 3.75
4 12% 3.35 3.5 3.6
5 11% 3.46 3.49 3.7
6 10% 3.7 3.75 3.75
7 18% 3.71 3.71 3.73
8 15% 2.93 3.71 3.71
9 4% 4 3.93 4
Average 100% 3.41 3.58 3.75
The formula is less important to me than the actual solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dec 18 2023 05:49 AM
<< The formula is less important to me than the actual solution >>
If you are thinking that there is one solution, that's wrong! At least, it's wrong, given the limited information (on constraints/boundaries/restrictions and relationships) that you have supplied to us. Mathematically, there are nine solutions, one for each of the nine variables (which are presumably independent, as you have not indicated otherwise)…but each of those nine solutions is dependent on the scores for the other eight concepts.
Again, the minimum score required for any concept depends upon the (weight and) score of every other concept. Grasp that. A person (or computer) can't determine the minimum for #1 without knowing (or assigning) values for #2-#9; a person (or computer) can't determine the minimum for #2 without knowing (or assigning) values for #1 and #3-#9. And so on.
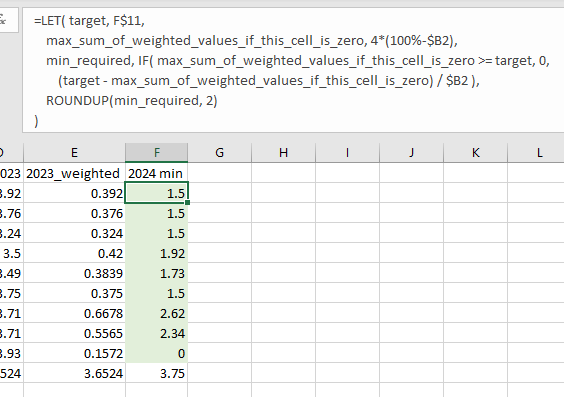
As you have written that scores can only be in the range 0 to 4, the numbers I provided in green on Sheet2 are the 9 solutions — the minimum scores* one can have for those concepts and still reach the target weighted score. But each — individually — can only apply if scores for all other concepts are at their maximums (of 4).
* in multiples of 0.01
In the newer attached workbook, I have added nine columns of content to Sheet2 to make this more obvious,
The best analogy for this situation I can think of is this:
You ask me to tell you which number between 1 and 1 thousand is most even. I then say that half of them (500) are even, so there are 500 such numbers, but you demand "one number". You have not specified sufficient constraints/boundaries/restrictions to arrive at just "one number".
Based on information you supplied, there are — among the 268 sextillion (268,101,567,757,470,981,763,601) possible combinations of scores — up to 111 trillion combinations of scores that might reach the target. Realistically, it's far, far less than 111 trillion, but no one is going to compute the validity of those combinations, much less determine (multiple) minimums among them. To reduce that number, you — or someone with knowledge of the problem domain — must devise additional constraints or boundaries or restrictions (choose your term) and/or limiting relationships between the scores, whether they are real or you make them up.
Maybe you have some ideas (vague or specific) of which possible values you want to check. To assist you in those checks, I created different minimization formulas on Sheet3. There you can enter whatever values you care about (for all 9 concepts under Scenario 0, or for 8 of the 9 concepts in the other scenarios) to see the results. And as on Sheet2, the cells highlighted in green will show the minimum score — rounded up to the next multiple of 0.01 — for that concept (row) with that combination of other, assigned concept scores (in the same column) required to reach the target.