Working with Binary numbers BASE(..., 2, 7) and bit operations BITXOR, BITAND

[Peter Bartholomew]

I recently came across an Excel challenge from Chinmay Amte on LinkedIn and I plan to post my solution here because it contains some 'off the beaten track' techniques that might be of some interest.

Post | Feed | LinkedIn
"Yesterday, Indian state of Bihar was in news due to change in structure of coalition government.
Assume you are an Analyst at Governor's office.  He has asked you to evaluate ALL possible combinations of coalition between the political parties to form a government."

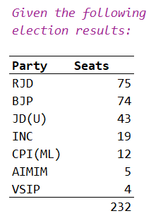
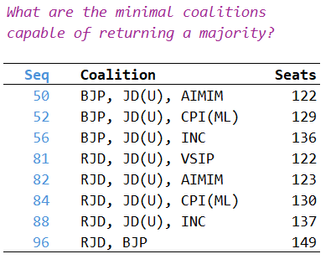
Please note, minimum vote of 122 is required to form government.
The correct answer for the number of possible combinations is 61 (done manually)!

There are 127 combinations so I started with a decimal index but, within the Lambda functions SeatCountλ and ListNamesλ, this is first turned into a binary number (with 1 indicating that the corresponding party is part of the coalition.

= LET(
    n,            COUNTA(party),
    combinations, SEQUENCE(2^n - 1),
    totalSeats,   MAP(combinations, SeatCountλ(seats)),
    possible,     FILTER(combinations, totalSeats>121),
    coalition,    MAP(possible, ListNamesλ(party)),
    seats,        MAP(possible, SeatCountλ(seats)),
    HSTACK(coalition, seats)
  )

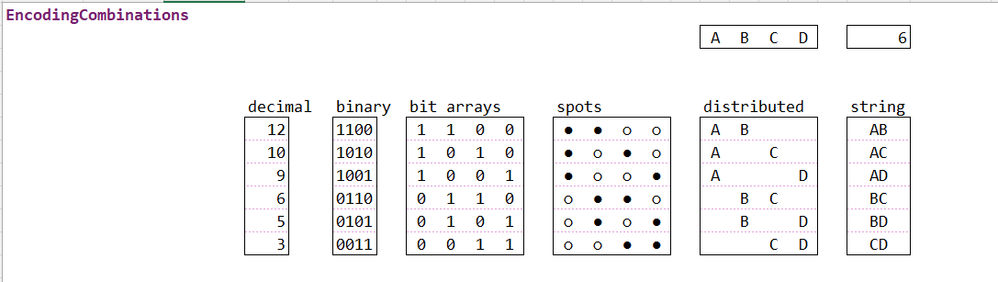
MID is then used to split the binary number (a string) into separate cells to that matrix multiplication can be used to evaluate the total seats for each coalition.

"SeatCountλ"
= LAMBDA(combination,
    LET(
        n,   COUNTA(seats),
        bin, BASE(combination, 2, n),
        k,   SEQUENCE(1, n),
        p,   SIGN(MID(bin, k, 1)),
        MMULT(p, seats)
    )
  )

I observed that the coalitions identified include cases that have more parties involved than are strictly necessary to form a government.  Therefore I set out to discount any coalition that included a viable governing coalition as a subset.  That is where the bit operations came into the equation.

Subsetλ
"Determines whether the first parameter is a subset of the second 
where set membership is determined by digits of a binary number"
= LAMBDA(set₁, 
    LET(
      diff, BITXOR(set₁, set₂), 
      IF(set₁ <> set₂, BITAND(set₁, diff) = 0)
    )
  )

Despite the fact that the concept involves binary numbers, the arguments to BITXOR and BITAND are actually their decimal equivalents.  Exclusive BITXOR returns 0 where the corresponding bits match and 1 for mismatches.  The bitwise BITAND examines one of the sets to see whether there is any non-zeros where the sets differ.  That is does that coalition include any parties that are not in the second, in which case both combinations must be retained.

It is not often I get to use BITXOR etc.  Do others have examples of their use?

Just as a final point which may cause reaction from Excel users that hate 'black boxes', my final worksheet formula was no more than

= PotentialCoalitionsλ(party,seats,122)

which gave rise to

I am happy to accept any feedback.  It is, after all, well away from looking like a traditional spreadsheet.

[#2]

@Peter Bartholomew 

Combinations is too complex for me, make the bookmark to play one day.

As for the binary logic long ago I used it to check if the character is in English alphabet or in digits

ABC = LAMBDA(chr,
    IFERROR(
        BITOR(chr, 48),
        IFERROR(CHAR(BITXOR(CODE(chr), 32)) = chr, 0)
    )
)

and only to play with it, sure could be done other way. No more practical cases in my practice.

[#3]

@Sergei Baklan 

Even that is more than I had expected!  I had definitely regarded BITXOR as lying within an exotic but very obscure corner of Excel.  Perhaps not as bad as a Bessel function of the second kind, but close.  Mind you, the finance formulas have their oddities; DOLLARFR means very little to me!

Presumably the trick in your formula is to move from lower case characters to upper case and the converse.

[#4]

Confession.

I have changed the code that checks whether a given proposed coalition contains a smaller viable coalition.  Originally I worked with arrays of the form {1,1,0,0,1,0,1} to check the subset condition and that required nested MAPs which were not pretty.  Since BITXOR and BITAND work with the decimal representation (i.e. scalars rather than arrays) that part could be simplified.

HasSubsetλ
"Tests whether each of an array of sets is a superset of the others"
= LET(
    q, TRANSPOSE(p),
    s, SIGN(IF(p <> q, BITAND(BITXOR(p, q), q) = 0)),
    BYROW(s, LAMBDA(x, SUM(x))) > 0
  )

Sadly, settling for the first thing that works has its shortcomings.

[#5]

@Peter Bartholomew 

Looks like a nice approach, I'd like to make time to check this out in more detail. It does makes me think a lambda function for generating combinations, like the one in Python, would make for a useful utility function and worth looking at as a future challenge.

On the subject of more obscure functions, I have seen specialised financial functions such as DOLLARFR and even ODDFYIELD employed in the context of treasury yield computations. Bitwise functions are also fairly niche in my experience but become more useful in lambda development where one is looking to optimise algorithms for example replacing array comparisons with bitwise operations. One application I have found myself reusing on multiple occasions is in generating (pseudo-)random data but removing volatility e.g. for benchmarking or speeding up recalc

=LAMBDA(length, [seed],
    TAKE(
        SCAN(
            IF(ISOMITTED(seed), 123456789, seed),
            SEQUENCE(length, , , 0) * {13, -17, 5},
            LAMBDA(s, i, BITXOR(s, BITAND(BITLSHIFT(s, i), 2 ^ 32 - 1)))
        ),
        ,
        -1
    )
)(5)

ref: https://en.wikipedia.org/wiki/Xorshift

[#6]

@Peter Bartholomew 

I've used BITXOR and BITAND very sparingly and I've played with BITLSHIFT and BITRSHIFT.  I understand what the functions do but have not used them enough to the point where I can conceptualize a solution for combinations/permutations.  I'll study your solution provided to see where I can find ways to make use of these functions.

My current way of tackling this task is with the help of DEC2BIN.  I understand the limitations involved but for 127 possibilities it's more than up to the task (for much more than 127 perhaps Python is the best option.)

'GenerateCombinations
=LAMBDA(party,seats,combinations,LET(
    header, HSTACK(TOROW(party), "Seats"),
    n, COUNT(seats),
    seq, SEQUENCE(n),
    combinations, SUM(COMBIN(n, seq)),
    BIN_vector, DEC2BIN(SEQUENCE(combinations), n),
    height, ROWS(BIN_vector),
    GetSeats, LAMBDA(r, c,
        LET(
            bin_val, MID(INDEX(BIN_vector, r), c, 1),
            seat_total, INDEX(seats, c),
            bin_val * seat_total
        )
    ),
    SeatMatrix, MAKEARRAY(height, n, GetSeats),
    CoalitionSeats, BYROW(SeatMatrix, SUM),
    CoalitionMatrix, FILTER(HSTACK(SeatMatrix, CoalitionSeats), CoalitionSeats >= required),
    Results, SORT(CoalitionMatrix, n + 1),
    VSTACK(header, Results)
))

[#7]

@lori_m 

Thank you. Amazingly compact, equally opaque!  

Pseudo random numbers are something of a closed book to me but could be useful nevertheless.

As you suggest, I can see me using them to generate test datasets without the volatility of RANDARRAY.

[#8]

@Patrick2788 

"but for 127 possibilities it's more than up to the task

(for much more than 127 perhaps Python is the best option)"

I wouldn't give up on the Excel formula language that easily.  BASE is good for numbers up to 2^53!  Mind you, I had never noticed that DEC2BIN has a 'places' parameter, so I could have used it.

I first saw it when @lori_m used it for a Chandoo minimum length formula challenge.  My recollection is that it was a case of multiplying by 37 in base 36 to double up the letter encoding a value.

[#9]

Peter - you have a better memory than me, it was only after ten minutes of searching I found this (Code Golf) formula for checking if a string contains a repeated character:

=COUNT(SEARCH(BASE(({0,1,2,3,4,5}+{0;1;2;3;4;5}*6)*37,36,2),A1))>0

I remember avoiding the dreaded CSE entry and unnecessary range dependencies introduced by ROW, etc. were an integral part of such challenges. Things are much more straightforward these days - Excel formulas being a bone fide language and all - though maybe not quite as fun :)

( https://dhexcel1.wordpress.com/2017/10/03/boolean-formula-for-repetitive-characters-in-a-string/ )

[#10]

I don't know whether to be more impressed by your original answer or by the fact that you can still find it!
BTW I have corrected a critical typo in my post.

[#11]

@Peter Bartholomew
you are (all) amazing for sure. wanted to impress you with a new approach solution but deadlocked myself into complexity. then at least some (hopefully) interesting conclusions for the next day when your manager in Governor's office ask back that "...ok great, but then what?" and you realise that the traveling agent problem came into the game as well. meaning that which party should send negotiators to where and first?

#1
RJD>>BJP
of course the first meeting can quickly close the coalition negotations

#2
RJD>>JDU
BJP>>JDU
decisive two meetings parallel. the top2 party, which is failing to cooperate with JDU, will surely fall out from coalition.

#3 (RJD)
RJD&JDU>>VSIP
now looking for the satellites, RJD&JDU core should agree with the most little party, which should be the "easiest" regarding the compromises made

#4 - #6 (RJD)
RJD&JDU>>AIMIM
RJD&JDU>>CPIML
RJD&JDU>>INC
if none of those talks is successful, then RJD wont be part of a coalition

#3 - #5 (BJP)
BJP&JDU>>AIMIM
BJP&JDU>>CPIML
BJP&JDU>>INC
the same as at #4 - #6 (RJD), with a tiny difference, that BJP will be never in coalition talks with VSIP, without a working constellation. with other words it is unnecessary to send negotiators from BJP to VSIP

[#12]

@Balint79 

Not quite a travelling salesman in that there is no obligation to visit all the parties?  That said, my calculations were intended to support the kind of analysis that you have provided.  I couldn't go further without knowing more about the internal politics of Bihar state.

[#13]

ooooh pseudo-random number. I totally thing Excel should add [seed] to RAND() and all of its 'sister' functions. That said I created my own pseudo-rand number generator (very primitive but fine for most non-scientific work) and will have to compare it to the option you give here.
I have seen many good options for pseudo-rnd numbers here on the forum when people ask to create 'random' lists for work schedules or baseball call sheets or tournement lists, etc... Having a SEED value based on the date, or week, or whatever will give them that random feel but not change every time they re-open the sheet. thx for sharing.

[#14]

@Peter Bartholomew

correct, however you do not have to know politics for such analysis as even salesmen did not know anything about Bernoulli's principle. regarding the rules it became just more exciting, as salesmen might have the chance to visit a place in the morning hours where they could sell all their stuff and finish for that day. such option would be definitely alluring to them. also any preliminary info about places to avoid (like Old Order Amish) due to less sales chances. hope you noticed that do not want to convince you, it is just about playing with rules via combining unexpected factors, eg is the smiley within the cube or not...?

       ⌜            ⌝
   ⌜           ⌝
       .    (:        ⌟

   ⌞           ⌟

[#15]

@m_tarler 

Maybe we need an archive folder to store the definitive recommendations and methods thought to be of long-term value?  I think a pseudo-random number generator would qualify.

[#16]

@m_tarlerYes, having a repeatable random function can come in handy, I've quite often divided by 2^32 to get a non-volatile RAND alternative

@Peter Bartholomew Indeed, another possible candidate might be a 'combinations' function,

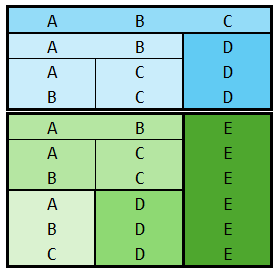
=combinations({"a";"b";"c";"d"},2)

which would return {"a","b";"a","c";"b","c";"a","d";"b","d";"c","d"}. I had been thinking about this off and on for a while but like @Sergei Baklan couldn't see any reasonable route. I revisited again in light of the bisection method you provided recently based on a recursion over an array version of,

COMBIN(n,k) = COMBIN(n-1,k-1) + COMBIN(n-1,k)

For example with the following lambda definition =combinations(sequence(20),10) returns COMBIN(20,10)*10=1847560 elements.

combinations
=LAMBDA(arr, k,
    IF(
        k <= ROWS(arr),
        IF(
            k = 1,
            arr,
            DROP(
                VSTACK(
                    combinations(DROP(arr, -1), k),
                    EXPAND(combinations(DROP(arr, -1), k - 1), , k, @TAKE(arr, -1))
                ),
                k = ROWS(arr)
            )
        )
    )
)

[#17]

Just to add I should have checked the archives before posting the above formula. Two good alternative methods that came up in search results were (not coincidentally by both aforementioned contributors)

https://techcommunity.microsoft.com/t5/excel/efficient-approach-to-generate-list-of-combinations-wit... 

https://techcommunity.microsoft.com/t5/excel/all-combinations-of-5-numbers-from-1-to-35/m-p/3717447/... 

Evidence that there are sufficient high quality examples available now to build general purpose libraries of lambdas.

[#18]

@lori_m 

That was quite an achievement!  I am not sure that my mind is correctly wired for recursion.  I did get there but it was far from easy.

I picked out one step in your recursive calculation and, at least, it explained why the manner in which the combinations are ordered is a little unusual.

The other thing I noticed was that various nested calculations are performed more than once.  I suppose that goes for the recursive formula for the count of combinations as well

COMBIN(n,k) 
= COMBIN(n-1,k-1) + COMBIN(n-1,k)
= COMBIN(n-2,k-2) + COMBIN(n-2,k-1) 
                  + COMBIN(n-2,k-1) + COMBIN(n-2,k)

Something else that had me puzzled for a moment was the type conversion

@TAKE(arr, -1)

used to pad the expanded array.

[#19]

@Peter Bartholomew 

I finally managed to take a look at your file attachment today and I think the BITXOR approach works well when applied to the problem of finding the minimal subsets for smaller data sets like the one in question. A couple of related thoughts occurred to me while looking through the lambda definitions...

1. To generate the list of possible sums one might also try:

=REDUCE(0,seats,LAMBDA(a,n,VSTACK(a,a+n))

which appears very efficient compared to MMULT [0.33s with seats=sequence(20)]. Within the LET definition, this modification returned equivalent results for me:

combinations, SEQUENCE(2^n,,0),
totalSeats, REDUCE(0,seats,LAMBDA(a,n,TOCOL(a+{0,1}*n)))

2. For generating the minimal subsets, I also tried recursion with a threshold condition. Binary trees appear pretty powerful and applicable to a wide range of problems - but as you suggest the main issue is trying to keep a clear head!

[#20]

@lori_m 

Thanks for the reply, I will study it.

Meanwhile, to place the ball back in your court, I have been working up an alternative approach to the generation of all combinations of m objects from n.  

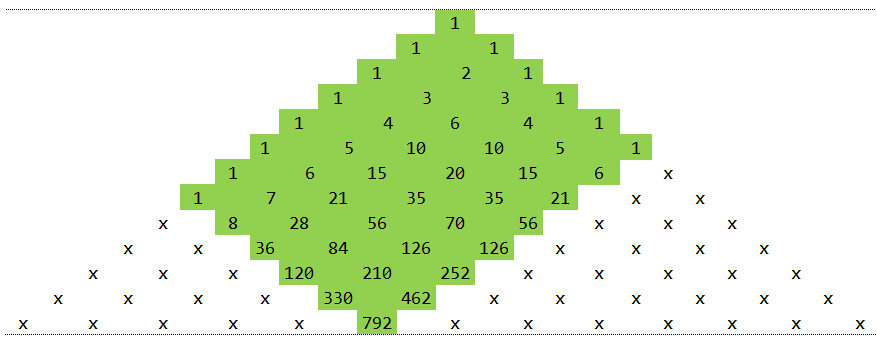
I loved the elegance bisection formula and the way sets were combined.  What troubled me was the duplication that was appearing.  In 'normal' family trees there are 4 second generation ancestors and 8 third generation; in this case the numbers are 3 and 4 respectively with ancestors in common on both branches of the tree.  This implies that  some calculations are performed multiple times.

What I tried instead was to SCAN one side of Pascal's triangle and use the thunked results to initialise reduction steps on the other diagonal.   The dimensions of the scanned region are m x (n-m)

I think I started out converting the function calls to @Craig Hatmaker 's 5g functions but I have yest to reach the end of that process!  I was happy to put the effort into the main program segments but wondered how far to go down the functional decomposition.  I remember Craig's Central Error Reporting for VBA the entire calling tree was documented and would be returnable to assist the developer whilst being suppressed for an end user with no access to the code.