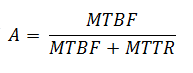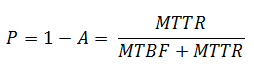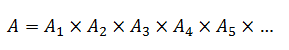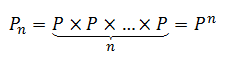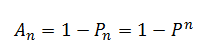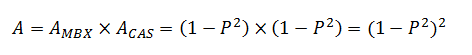Definitions
We all know that in the Microsoft Exchange world DAG stands for “Database Availability Group”.
Database – because on a highly available Exchange 2010 Mailbox server, the database, not the server, is the unit of availability and it is the database that can be failed over or switched over between multiple servers within a DAG. This concept is known as database mobility.
Group – because the scope of availability is determined by Mailbox servers in a DAG combined in a failover cluster and working together as a group.
Availability – this word seems to be the least obvious and the most obfuscated term here (and also referred to by both other terms). Ironically, it has a straightforward mathematical definition and plays an important role in understanding overall Exchange design principles.
Wikipedia defines “availability” to mean one of the following:
- The degree to which a system, subsystem, or equipment is in a specified operable and committable state at the start of a mission, when the mission is called for at an unknown, i.e., a random, time. Simply put, availability is the proportion of time a system is in a functioning condition. This is often described as a mission capable rate. Mathematically, this is expressed as 1 minus unavailability.
- The ratio of (a) the total time a functional unit is capable of being used during a given interval to (b) the length of the interval.
Using terms of probability theory, both of these definitions mean the same: probability that a given system or component is “operable” or “capable of being used” (i.e. available) at any random moment of time (when we test it).
Mathematically this can be measured by calculating the amount of the time when system is available (“uptime”) during some large statistically representative period (typically a year), and dividing it by the total length of the period. Using the widely adopted terms of Mean Time Between Failures (MTBF) and Mean Time To Repair (MTTR) – the former represents system availability / uptime between the failures, while the latter represents system downtime during any given failure, – availability can be expressed as a fraction:
The opposite mathematical characteristic would be a probability of failure (think “non-availability”):
Availability is often expressed as “number of nines”, according to the following table:
| Availability level | Availability value | Probability of failure | Accepted downtime per year |
| Two nines | 99% | 1% | 5256 minutes = 3.65 days |
| Three nines | 99.9% | 0.1% | 525.6 minutes = 8.76 hours |
| Four nines | 99.99% | 0.01% | 52.56 minutes |
| Five nines | 99.999% | 0.001% | 5.26 minutes |
Of course, the availability value would be different depending on whether we take into account both scheduled (planned) and unscheduled (unplanned) downtime or just unscheduled downtime only. The Service Level Agreement that represents business availability requirements must be very specific about it. But in all cases availability of any given system or component depends on many factors, and it is utterly important to identify and understand these dependencies and how they impact availability.
How service dependencies impact availability
The availability of an Exchange mailbox database depends on the availability of many other services and components – for example, the storage subsystem that hosts the database, the server that operates this database, network connectivity to this server, etc. All of these are critical components, and the failure of any single one of them would mean loss of service even if the database itself is perfectly healthy. This means that in order for the database to be available as a service, every single dependency of the data base must be available as well. If we properly identify and isolate the dependency components, we can mathematically calculate how they determine the resulting availability of the Exchange mailbox database itself.
For a given Exchange mailbox database, the following components could be considered critical dependencies:
- Database disk / storage subsystem – let’s say its availability is A1;
- Mailbox server (both hardware and software components) – say its availability is A2;
- Client Access Server (both hardware and software components) – remember that in Exchange 2010 all clients connect to mailbox database only via Client Access Server, and let’s assume CAS is installed separately from the Mailbox server in this case – say its availability is A3;
- Network connectivity between clients and the Client Access Server, and between the Client Access Server and the Mailbox server – say its availability is A4;
- Power in the datacenter where servers and storage are located – say its availability is A5;
This list could be continued… For example, Active Directory and DNS both represent critical dependency for Exchange as well. Moreover, in addition to pure technological dependencies, availability is impacted by process dependencies such as operational maturity and so on: human error, incorrectly defined operations, lack of team coordination could all lead to service downtime. We will not try to compile any exhaustive list of dependencies here but instead focus on how they impact overall service availability.
Since these components themselves are individually independent of each other, the availability of each of them represents an independent event, and the resulting availability of an Exchange mailbox database represents a combination of all these events (in other words, in order for a mailbox database to be available to clients all of these components must available). From the probability theory, the probability of a combination of independent events is a product of the individual probabilities for each event:
For example, if you toss three coins, the probability of getting heads on all three coins is (1/2)*(1/2)*(1/2) = 1/8.
It is important to realize that since each individual availability value cannot be larger than 1 (or 100%), and the resulting service availability is simply a product of individual component availabilities, the resulting availability value cannot be larger than the lowest of the dependent component availabilities.
This can be illustrated with the example presented in the following table (the numbers here are samples but pretty realistic):
| Critical dependency component | Probability of failure | Availability value |
| Mailbox server and storage | 5% | 95% |
| Client Access Server | 1% | 99% |
| Network | 0.5% | 99.5% |
| Power | 0.1% | 99.9% |
| Overall service (depends on all of the above components) | 6.51383% | 95% x 99% x 99.5% x 99.9% = 93.48617% |
From this example, you can see how critically important service dependencies are. Even for a mailbox database that never fails (never gets corrupted, never gets any virus infection etc.), availability still remains below 93.5%!
Conclusion: A large number of service dependencies decreases availability.
Anything you can do to decrease the number or impact of service dependencies will positively impact overall service availability. For example, you could improve operational maturity by simplifying and securing server management and optimizing operational procedures. On the technical side, you can try to reduce the number of service dependencies by making your design simpler – for example, eliminating complex SAN based storage design including HBA cards, fiber switches, array controllers, and even RAID controllers and replacing it with a simple DAS design with a minimum of moving parts.
Reduction in service dependencies alone might not be sufficient enough to bring the availability to the desired level. Another very efficient way to increase the resulting availability and minimize the impact of critical service dependencies is to leverage various redundancy methods such as using dual power supplies, teamed network cards, connecting servers to multiple network switches, using RAID protection for operating system, deploying load balancers for Client Access servers and multiple copies of mailbox databases. But how exactly does redundancy increase availability? Let’s look more closely at load balancing and multiple database copies as important examples.
How redundancy impacts availability
Conceptually all redundancy methods mean one thing: there is more than one instance of the component that is available and could be used either concurrently with other instances (as in load balancing) or as a substitution (as in multiple database copies). Let’s assume we have n instances of a given component (n servers in a CAS array, or n database copies in a DAG). Even if one of them fails, the other instances can still be used thus maintaining availability. The only situation when we will face actual downtime is when all instances fail.
As defined earlier, the probability of failure for any given instance is P = 1 – A. All instances are statistically independent of each other, which means that availability or failure of any of them does not im pact availability of the other instances. For example, the failure of a given database copy does not impact the probability of failure for another copy of that database (a possible caveat here could be logical database corruption propagating from the first damaged database copy to all other copies, but let’s ignore this highly unlikely factor for now – after all, you can always implement a lagged database copy or a traditional point-in-time backup to address this).
Again using the same theorem of probability theory, the probability of failure of a set of n independent components is a product of the probabilities for each component. As all components here are identical (different instances of the same object), product becomes a power:
Apparently, as P < 1, Pn is less than P, which means that probability of failure decreases, and correspondingly, availability increases:
Let’s consider some real life example for clarity. Say, we are deploying multiple mailbox database copies; each copy is hosted on a single SATA drive. Statistically, the failure rate of SATA drives is ~5% over a year[1], which gives us 5% probability of failure: P = 0.05 (which means availability of 95%: A = 0.95). How will availability change as we add more database copies? Look at the following table which should be self-explanatory:
| Number of database copies | Probability of failure | Availability value |
| 1 | P1 = P = 5% | A1 = 1 – P1 = 95% |
| 2 | P2 = P2 = 0.25% | A2 = 1 – P2 = 99.75% |
| 3 | P3 = P3 = 0.0125% | A3 = 1 – P3 = 99.9875% |
| 4 | P4 = P4 = 0.000625% | A4 = 1 – P4 = 99.9994% |
Pretty impressive, isn’t it? Basically, each additional database copy on SATA drive introduces the multiplication factor of 5% or 1/20, so the probability of failure becomes 20 times lower with each copy (and, correspondingly, availability increases). You can see that even with the most unreliable SATA drives deploying just 4 database copies brings database availability to five nines.
This is already very good, but can you make this even better? Can you increase availability even further without making architectural changes (e.g. if adding yet another database copy is out of the question)?
Actually, you can. If you improve the individual availability of any dependency component, it will factor in increasing overall service availability, and lead to a much stronger effect from adding redundant components. For example, one possible way to do this without breaking the bank is to use Nearline SAS drives instead of SATA drives. Nearline SAS drives have an annual failure rate of ~2.75% instead of ~5% for SATA. This will decrease the probability of failure for the storage component in the calculation above and therefore increase overall service availability. Just compare the impact from adding multiple database copies:
- 5% AFR = 1/20 multiplication factor = each new copy makes database failure 20 times less likely.
- 2.75% AFR = 1/36 multiplication factor = each new copy makes database failure 36 times less likely.
This significant impact that additional database copies have on database availability also explains our guidance around using Exchange Native Data Protection which says that multiple database copies could be replacement for traditional backups if a sufficient number (three or more) of database copies is deployed.
The same logic applies to deploying multiple Client Access servers in a CAS array, multiple network switches, etc. Let’s assume we have deployed 4 database copies and 4 Client Access servers, and let’s revisit the component availability table that we analyzed earlier:
| Critical dependency component | Probability of failure | Availability value |
| Mailbox server and storage (4 copies) | 5% ^ 4 = 0.000625% | 99.999375% |
| Client Access Server (4 servers, installed separately) | 1% ^ 4 = 0.000001% | 99.9 99999% |
| Network | 0.5% | 99.5% |
| Power | 0.1% | 99.9% |
| Overall service (depends on all of the above components) | 0.6% | 99.399878% |
You can see how just because we deployed 4 Client Access servers and 4 database copies, the probability of failure of the overall service has decreased more than 10-fold (from 6.5% to 0.6%) and correspondingly service availability increased from 93.5% to a much more decent value of 99.4%!
Conclusion: Adding redundancy to service dependencies increases availability.
Putting the pieces together
An interesting question arises from the previous conclusions. We’ve analyzed two different factors that impact overall service availability in two different ways and have found two clear conclusions:
- adding more system dependencies decreases availability
- adding redundancy to system dependencies increases availability
What happens if both are factors of a given solution? Which tendency is stronger?
Consider the following scenario:
We deploy two mailbox servers in a DAG with two mailbox database copies (one copy on each server), and we deploy two Client Access servers in a load-balanced array. (For simplicity, we’ll only consider the availability of a mailbox database for client connections, leaving Hub Transport and Unified Messaging out of consideration for now). Assuming that every server has its individual probability of failure of P, will the availability of such a system be better or worse than the availability of a single standalone Exchange server with both the Mailbox and Client Access server roles deployed?
In the first scenario, the Mailbox servers are independent and will be unavailable only if both servers fail. The probability of failure for the set of two Mailbox servers will be P × P = P2. Correspondingly, its availability will be AMBX = 1 – P2. Following the same logic, CAS services will be unavailable only if both Client Access servers fail, so the probability of failure for the set of two Client Access servers will be again P × P = P2, and correspondingly, its availability will be ACAS = 1 – P2.
In this case, as you may have realized, two Mailbox servers or two Client Access servers are examples of redundant system components.
Continuing with this scenario… In order for the entire system to be available, both sets of servers (set of Mailbox servers and set of Client Access servers) must be available simultaneously. Not fail simultaneously but be available simultaneously, because now they represent system dependencies rather than redundant components. This means that overall service availability is a product of availabilities for each set:
Of course, the second scenario is much simpler as there is only one server to consider, and its availability is simply A = 1 – P.
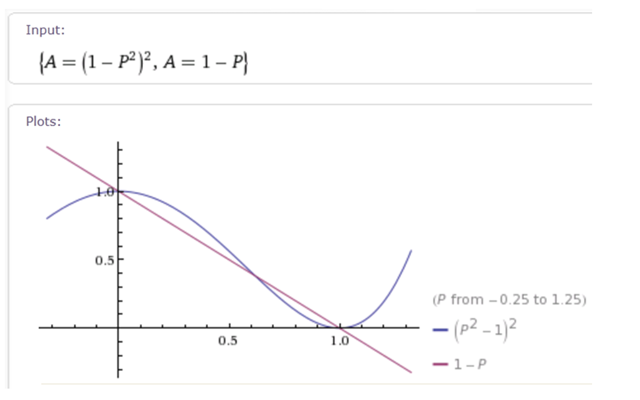
So now that we calculated the availability values for both scenarios, which value is higher, (1-P2)2 or 1-P?
If we plot the graphs of both functions, we’ll see the following behavior:
(I used the Wolfram Alpha Mathematica Online free computational engine to do the plotting quickly and easily).
We can see that for the small values of P, the availability of the complex 4-server system is higher than the availability of the single server. There’s no surprise; this is what we expected, right? However, at P ~ 0.618 (more precisely, ![]() ) the two plots cross, and for larger values of P the single server system actually has higher availability. Of course you would expect the value of P to be very close to zero in real life; however, if you are planning to build your solution from very unreliable components, you would probably be better with a single server.
) the two plots cross, and for larger values of P the single server system actually has higher availability. Of course you would expect the value of P to be very close to zero in real life; however, if you are planning to build your solution from very unreliable components, you would probably be better with a single server.
Impact of failure domains
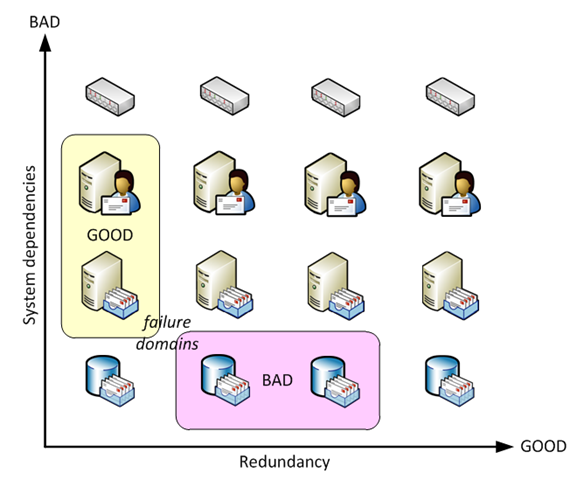
Unfortunately, real life deployment scenarios are rarely as simple as the situations discussed above. For example, how does service availability change if you deploy multi-role servers? We noticed in the scenario above that combining the server roles effectively reduces the number of service dependencies, so it would probably be a good thing? What happens if you place two database copies of the same database onto the same SAN array or DAS enclosure? What if all of your mailbox servers are connected to the same network switch? What if you have all of the above and more?
All of these situations deal with the concept of failure domains. In the examples above, server hardware, or a SAN array, or a network switch represent a failure domain. Failure domain breaks independence or redundancy of the components that it combines – for example, failure of server hardware in a multi-role server means that all Exchange roles on this server become unavailable; correspondingly, failure of a disk enclosure or a SAN array means that all database copies hosted on this enclosure or array become unavailable.
Failure domains are not necessarily a bad thing. The important difference is what kind of components constitute a failure domain – are they different system dependencies or are they redundant system components. Let’s consider two of the above examples to understand this difference.
Multi-role server scenario
Let’s compare availability of the two different systems:
- Both Mailbox and Client Access server roles hosted on the same server which has the probability of hardware failure of P;
- The same roles hosted on two separate servers, each having the same probability of hardware failure;
In the first case, hardware of a single server represents a failure domain. This means that all hosted roles are either all available or all unavailable. This is simple; overall availability of such a system is A = 1 – P.
In the second case, overall service will be available only when both servers are available independently (because each role represents a critical dependency). Therefore, based on probability theory, its availability will be A × A = A2.
Again, as A < 1, it means that A2 < A, so in the second case availability will be lower.
Apparently, we can add other Exchange server roles (Hub Transport and Unified Messaging if necessary) to the same scenario without breaking this logic.
Conclusion: Collocation of Exchange server roles on a multi-role server increases overall service availability.
Shared storage scenario
Now let’s consider another failure domain scenario (two database copies sharing the same storage array), and compare database availability in the following two cases:
- Two database copies hosted on the same shared storage (SAN array or DAS enclosure), which has the probability of failure of P;
- The same database copies hosted on two separate storage systems, each having the same probability of failure;
In the first case, shared storage represents a failure domain. As in the previous scenario, this means that both database copies are available or unavailable simultaneously, so the overall availability is again A = 1 – P.
In the second case, overall service will be available if at least one system is available, and unavailable only if both systems fail. The storage systems in question are independent; therefore, the probability of failure for the overall service is P × P = P2, and correspondingly overall service availability is A = 1 – P2.
Again, as P < 1, it means that P2 < P, and hence 1 – P2 > 1 – P. This means that availability in the second case is higher.
Conclusion: Collocation of database copies on the same storage system decreases overall service availability.
So what is the difference between these two scenarios, why does introducing a failure domain increase availability in the first case and decrease availability in the second?
It’s because the failure domain in the first case combines service dependencies, effectively decreasing their number and therefore improving availability, whereas the failure domain in the second case combines redundant components, effectively decreasing redundancy and therefore impairing availability.
All these concepts and conclusions could be probably visualized as follows:
(No we did not use Wolfram Alpha to draw this graph!)
Summary
Exchange 2010 architecture provides powerful possibilities to add redundancy at the Exchange level (such as deploying multiple database copies or multiple Client Access servers in a CAS array) and to decrease the number of system dependencies (by combining Exchange server roles in a multi-role server or using simpler storage architecture without an excessive number of critical components). The simple rules and formulas presented in this article allow you to calculate the effect on the availability value from deploying additional database copies or from combining Exchange server roles; you can also calculate the impact of failure domains. It is important to note that we tried to use these simple mathematical models to illustrate the concepts, not to pretend to obtain precise availability values. Real life rarely fits the simple basic scenarios, and you need much more complex calculations to get reasonable estimates for the availability of your actual systems; it might be easier to simply measure the availability statistically and verify if it meets the SLA requirements. However, understanding the factors that impact availability and how they play together in a complex engineering solution should help you design the solution properly and achieve a significant increase in overall service availability meeting even the most demanding business requirements.
Boris Lokhvitsky
Delivery Architect
[1] The following studies by Carnegie Mellon University, Google, and Microsoft Research show 5% AFR for SATA drives:
http://www.usenix.org/events/fast07/tech/schroeder/schroeder.pdf
http://labs.google.com/papers/disk_failures.pdf
http://research.microsoft.com/research/pubs/view.aspx?msr_tr_id=MSR-TR-2005-166
 Microsoft
MicrosoftYou Had Me at EHLO.