Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
- Home
- Windows
- Windows Insider Program
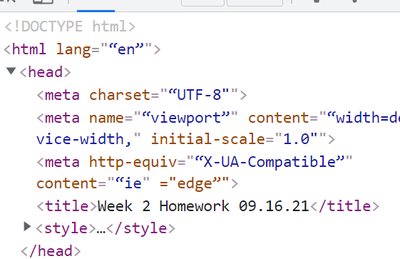
- open file from the File Manager to run my WebSite Code, it puts curly """'s in <head> and ruins code
open file from the File Manager to run my WebSite Code, it puts curly """'s in <head> and ruins code
Discussion Options
- Subscribe to RSS Feed
- Mark Discussion as New
- Mark Discussion as Read
- Pin this Discussion for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 17 2021 06:29 PM
I did not enter all those quotes. This is my code:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>Week 3 Practice</title>
<style>
h1 {
color: #1a64d6;
font-size: 64px;
line-height: 60px;
margin: 0 auto;
text-align: center;
padding: 20px;
}
h2 {
margin: 0 auto;
font-size: 34px;
line-height: 48px;
font-weight: 400;
text-align: center;
padding: 20px;
}
hr {
max-width: 900px;
}
body {
background: moccasin;
}
button {
display: block;
margin: 20px auto;
border: 1px solid #1a64d6;
background: #1a64d6;
color: #fff;
font-size: 16px;
line-height: 22px;
padding: 16px 24px;
border-radius: 30px;
transition: all 200ms ease;
box-shadow: rgba(37, 39, 89, 0.08) 0px 8px 8px 0;
cursor: pointer;
}
img {
max-width: 750px;
display:block;
text-align: center;
margin: 0 auto;
}
p {
margin: 10px 0;
padding: 5px;
border: 1px solid #999;
}
</style>
</head>
<body>
<br />
<br />
<h1>
<em> Wedding Lace </em>
</h1>
<br />
<br />
<h2>An Heirloom Throughout the Centuries</h2>
<br />
<br />
<p>Made to order lace tablecloth. This one fits table top 4' x 8'. Finished
product is 5' x 9' with lace edge. Lace edge is specifically made to order
with your words, names, or your meaningful phrases "word count will be
calculated by me and then discussed with you". Each custom tablecloth has
a different word count. The bigger the size the more words can be fit into
the edge. Takes approximately 3 weeks make the size that is shown.
Obviously a tableclothed for a table that sits 16 will take longer, but
I'm ready for that. Especially if the buyer does not want any words, just
the lace edge.
</p>
<p>I am excited about my product. I've sold two tablecloths
for a table that sits 24, for two very famous granddaughter of a famous
wine family. Had to sign a confidentiality agreement not to disclose
client. But, I got invited for dinner to see my product being used and
they had invited Martha Stewart. It was really fun. Martha was impressed.
Made a few more sales after that.
</p>
<p>Anyway, order your heirloom lace product. Lace typically last about 100 years with care.
I also include a documented letter that discusses, my threads, my 100 years old steel needles
in inherited from my grandmother who also inherited them from her grandmother. I also write in
how the tablecloth came to be, such as; "Commissioned by, and/or designed
by brides parents "and name them". Things like that.
</p>
<p>Documented history increases the
value of a textile. I once took an order from a grandmother who passed
away before her granddaughters wedding. Everyone was thrilled, and crying
including me, when they opened her Commissioned gift with her handwriting on a note.
It had her favorite bible phrases, and each of their first names. The note had the date
she ordered it.
</p>
<h3>Order yours. Write me here if you want
more details. Warm Regards, Rose
</h3>
</p>
<br />
<br />
<a href="https://www.etsy.com/listing/471267212/lace-tablecloth?ref=shop_home_active_1" class="Learn more at shop">
Learn More Now. You'll Love It! </a>
<p>
"Coded by:"
<em>
<strong>Rose Brians</strong>
</em>
</p>
</script>
</body>
</html>
I'm new and desparate. Windows can't help. Microsoft can't help. My college professor won't help. Does anyone have an answer, or can put me in touch with someone? Rose rbrians@outlook.com
0 Replies