- Home
- Microsoft 365
- Excel
- Using Solver to solve selling price and quantities to achieve the target amount
Using Solver to solve selling price and quantities to achieve the target amount
- Subscribe to RSS Feed
- Mark Discussion as New
- Mark Discussion as Read
- Pin this Discussion for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Feb 08 2022 02:45 AM
Hello guys,
Am trying to solve a task I was issued by a client yesterday. Am basically trying to solve for what is the best selling price for each unit and how much quantity can one sell in order to reach the target amount that was set. Am not coming from an economics background but an amateur learning through the community. I've checked you tube for the best possible example to help me solve it but no juice. Your assistance will be highly appreciated.
regards.
| Product Name* | Cost Price | Selling Price | Quantity | ||||||
| Spinach Bunch | 30 | 1 | Target Amount | 62500 | |||||
| Kales | 25 | 1 | |||||||
| Green Hoho | 80 | 1 | |||||||
| Tomatoes | 60 | 1 | |||||||
| Onions | 65 | 1 | |||||||
| Cabbage | 60 | 1 | |||||||
| Carrots | 60 | 1 | |||||||
| Potatoes Sack 50 Kg | 2500 | 1 | |||||||
| Fresh Beef Bones | 400 | 1 | |||||||
| Boneless Fresh Beef | 450 | 1 | |||||||
| Eggs Tray | 305 | 1 | |||||||
| Smokies | 370 | 1 | |||||||
| Green Peas (Shelled) | 200 | 1 |
- Labels:
-
Excel
-
Formulas and Functions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Feb 08 2022 06:13 AM
Your problem has no well-defined optimum. For example, if your selling price were 50% higher than the cost price, you could meet your target by selling 4000 spinach bunches and a sack of spuds. Somewhat improbable, but not ruled out by your model.
What is missing is the link between selling price and volume sold. The latter normally falls as the former increases, giving a maximum somewhere along the line.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Feb 08 2022 07:09 AM - edited Feb 08 2022 09:00 AM
@alvinro wrote: ``what is the best selling price for each unit and how much quantity``
First, you need to understand that this is not a simple problem. It falls into the category called "linear programming". And it often difficult to set up the constraints of the problem so that it can be solved.
Second, to that end, you need to define what you mean by "best". For example, do you require a minimum of 1 of each quantity? What is the maximum of each quantity? Do you have a minimum and maximum for the selling price of each item sold?
(Cost is not always the minimum selling price, unless of course you want to make that a constraint.)
(It seems odd that you can vary both. As a consumer, usually the selling price is out of our control. As a seller, usually the quantity is out of our control.)
For use with Solver, you might set up a target cell with a formula of the form
=(H2 - SUMPRODUCT(C2:C14, D2:D14))^2 , then specify Set ... To: Min in Solver.
Essentially, we want to minimize the absolute value of the difference -- unless you do not want to exceed the target amount. But Solver does not always work well with the ABS function. Squaring the difference is a way to accomplish the same thing without using ABS.
-----
PS.... I might add that in my experience, Solver does not do well with min-max problems with more than two variables. First, I can usually demonstrate with a counter-example that the result is __not__ a min or max. Second, often I just get an error from Solver -- either a complaint about the set-up, or a failure to find a solution. But both issues might simply be due to my ineffectiveness at setting up LP problems, in the first place.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Feb 08 2022 07:26 AM
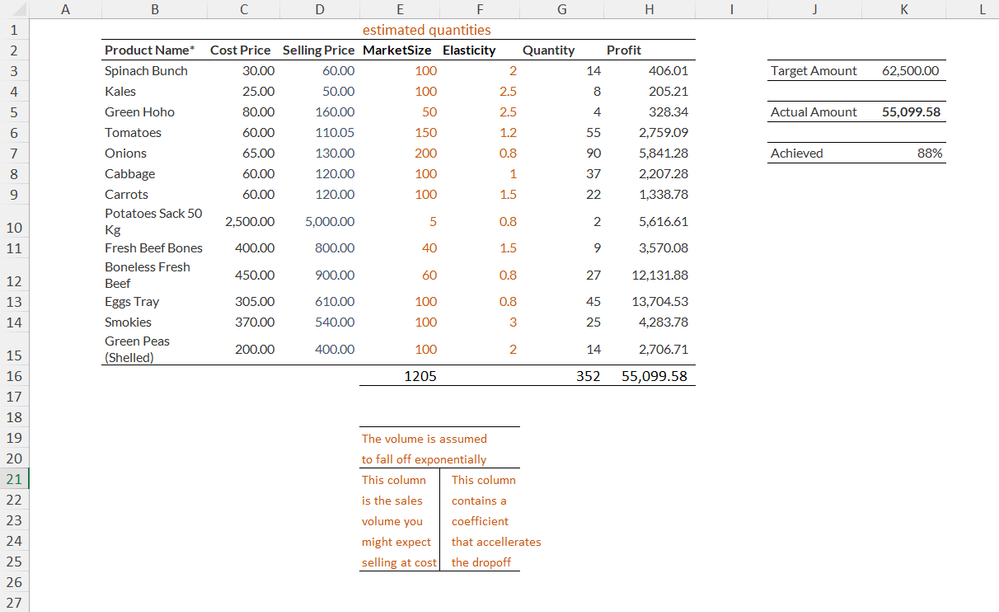
To illustrate the idea, I have assumed a volume of sales at cost and applied an exponential drop-off in volume as the price increases. I am not an economist so how good these assumptions may be is out of my area. I have allowed non-integer sales volumes to avoid unnecessary discontinuities that will upset Solver.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Feb 08 2022 09:43 AM
First thank you for the reply, it's my debut in this forum. I have to admit this is not as easy as I thought. I accepted the job offer thinking I would find a quick easy solution to accomplish the task. After reading the comments, I've looked at the question more critically, checked out LP and it demands a lot for an amateur... not demeaning myself lol. Yes, formulating an effective LP is the backbone to solving these problems.
From your gist I've learnt a lot... so something like the cost price doesn't necessarily mean it's supposed to be the minimum price which I assumed to be so. From what I've understood now.. I did not include that the first constraint is that: selling price > cost price and the second constraint is: quantity > 0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Feb 08 2022 09:58 AM
Thanks for the prompt response ..I must admit I didn't really understand what I was getting myself into after reading Joe's gist I went and checked what's really required of the problem and it ain't as simple as I thought for an amateur. LP really demands a lot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Feb 08 2022 10:57 AM - edited Feb 09 2022 07:30 AM
@alvinro wrote: ``I accepted the job offer thinking I would find a quick easy solution to accomplish the task.``
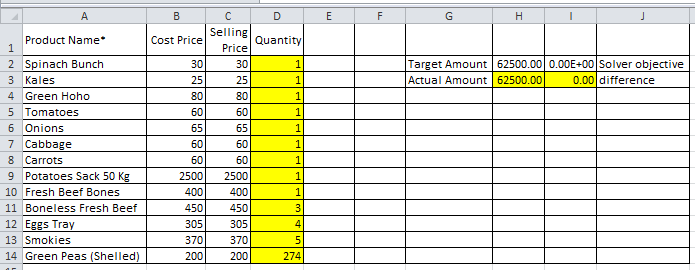
And perhaps there is. See the attached file for some simple models.
In the first model (worksheet "orig"), I allow both selling price and quantity to vary, with a minimum of constraints. I assume that quantity must be integers; but it is unclear if that constraint is valid for all items (e.g. if quantity is a measure of weight). This is the result.
Note that I changed the objective formula in I2. Based on the assumption that the actual amount should not exceed the target amount, the formula in I2 is simply:
=H2-SUMPRODUCT(C2:C14,D2:D14)
Also note that the Solver objective formula in I2 depends on the unrounded selling price (column C), whereas the actual amount in H3 depends on the rounded selling price (column E). We should not reference column E in I2 because often, Solver cannot tolerate rounded amounts.
(It is "dumb luck" when Solver works despite the use of rounded amounts and other functions that cause "discontinuities" -- non-smooth variations as variables are changed.)
-----
However, considering how close the derived selling prices are to "cost", I reiterate that I suspect that "cost" should really be the selling price. So, in the second model (worksheet "quant only"), I allow only quantity to vary. This is the result:
Note the significant difference.
Disclaimer: There might be multiple solutions that are either the same or "good enough". I have not made any effort to explore that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Feb 09 2022 05:57 AM
Thank you for the effort and time... Yes yes, the quantity must not be float forgot to mention that cause we are selling per unit of the product and not the weight per se... At least now I know how to go about it... I appreciate.