- Home
- Microsoft 365
- Excel
- Time Weighted Rate of Return using dates
Time Weighted Rate of Return using dates
- Subscribe to RSS Feed
- Mark Discussion as New
- Mark Discussion as Read
- Pin this Discussion for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 29 2021 01:45 AM
Dear community,
I'm trying to make a formula for a time weighted rate of return, in other words: I want to see my current account development in percent where deposits are weighted for whence they are added to the account. (This is usually what is displayed on your securities account in your bank).
In this case I want the formula to be for the current year 2021, I've got arbitrary dates with the corresponding account value, deposits are seen in column C. I would like to calculate and update value of the time weighted rate of return for each row.
I've been trying without any success and turns to the crowd for advice and guidance - the math and Excel-programming are above me.
See below for example of input. Just ask if anything need to be clarified.
- Labels:
-
Excel
-
Office 365
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 29 2021 02:59 AM - edited Jul 29 2021 03:23 AM
I myself have limited or no idea about the subject.
I can still add up my capital in my head ... is no more than my trouser pocket can carry :))).
Whatever the case, here is a link with very good information and possibilities with examples.
Time Weighted vs. Money Weighted Returns
Capital-weighted return, also: money-weighted return, internal rate of return (IZF), internal rate of return (IRR)
Time-weighted rate of return, also: time-weighted rate of return (TWROR) or true time-weighted rate of return (TTWROR)
Additional formula:
The formula for calculating the absolute interest income (in euros) for every deposit / withdrawal:
Interest income = B13 * POWER ((1 + $ G $ 3), E13) -B13
In which:
B13 = capital inflow / withdrawn on day X in €
$ G $ 3 = assumed (accumulated) annual interest rate in%
E13 = years since capital was used / withdrawn
I would be happy to know if I could help.
Nikolino
I know I don't know anything (Socrates)
* Kindly Mark and Vote this reply if it helps please, as it will be beneficial to more Community members reading here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 29 2021 03:52 AM - edited Jul 29 2021 03:53 AM
IMHO, the term "time-weighted" rate of return is misleading because there is nothing "weighted" nor "time-valued" about the calculation.
It would have been nice if you had attached an Excel file; or at least if you had shown row and column labels. It also would have been nice if you had labeled or explained the values in each column.
Finally, an example of the __form__ of the desired result would have been nice, even if the values were mocked up and incorrect.
I assume the following:
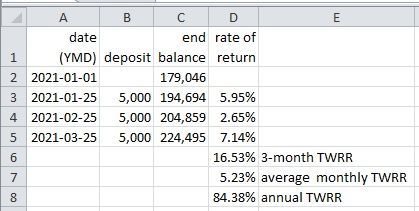
Formulas:
D3: =(C3 - B3) / C2 - 1
D6: { =PRODUCT(1 + D3:D5) - 1 }
D7: =(1 + D6)^(1/3) - 1
D8: =(1 + D6)^4 - 1
I assume the deposit is added to the account at the end of the period, after the gain or loss is added to the balance each month. So the formula in D3 (copied into D4 and D5) subtracts the deposit from the ending balance in order to calculate the monthly rate of return.
(The calculation would be different -- and simpler -- if the deposit is added at the beginning of each period.)
The cumulative 3-month TWRR is the product of the periodic rates of return, shown in D6.
In this case, the periodic rates of return are calculated on a regular basis (i.e. monthly). But that is not necessary. The TWRR would be calculated the same way if the dates on the left were irregular.
Note that the formula in D6 is array-entered by pressing ctrl+shift+Enter. Do not type the curly braces; Excel adds them when displaying the formula. (I use Excel 2010. In Excel 365 and later versions, it might not be necessary to press ctrl+shift+Enter.)
The average monthly TWRR is calculated in D7.
IMHO, the calculations should stop there. That is, for less than one year's worth of data, we should only calculate a cumulative TWRR or an average periodic TWRR.
However, some people believe that we can annualize sub-annual rates of return by compounding. That calculation is shown in D8. IMHO, that is misleading
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 29 2021 06:18 AM
Thank you for your time and input. I had already looked at similiar sites but without success. The issue for me is that my time periods are not set and more arbitrary. Deposits are not necessarily at set dates and some months there may be no deposits, or even two.
My thought is that I should incorporate the lapsed time each time and work in increments, but I'm not sure how to do it. My tries were unsuccessfull.
/Q
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 29 2021 06:38 AM
Hi and thank you for your thorough answer. I'm sorry for the scare information, the provided excel sheet is just an extract of a larger file and not in English and I wanted to limit the data. You were correct in your assumptions regarding the column data.
I do agree that it would be simpler if the deposits were made once a month and in set date, but one of my issues here is that I want to be able to make a deposit arbitrarily and still get a correct rate of return - I'm aiming to find a way to calculate it basically the same way my bank does, i.e. incorporate the effects of my deposits and their reduced market exposure.
I may add that I'm not sure if I used the correct annotation, I'm not an economist, nor is my first language English, so there may have been some lost in translation in both planes. But basically, what I want is a way to correctly display my interest development. So I may not be using the correct terminology, but I do want to weigh my balance with the lapsed time. I hope I am making sense.
Correct me if I'm wrong, but if I want to use your provided formula - I need to extract the dates for deposits? If there are several deposits in a month, how do I account for that?
I have attached a sheet with the raw data. If other metadata is necessary, I can probably provide that as well. The format is the same as follows, where the rows with deposits are marked green.
Regards
/Q
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 29 2021 08:29 AM - edited Jul 29 2021 12:51 PM
Solution
Just to clarify.... I was not suggesting any change in your format or frequency of data. It was not clear to me what problem you wanted to solve. So my intention was only to demonstrate the TWRR calculation. I should have made that clear the first time. Sorry.
-----
Re: ``I'm aiming to find a way to calculate it basically the same way my bank does``
To that end, it would be helpful to see what the "bank" calculates, and how it is reported.
Re: ``nor is my first language English, so there may have been some lost in translation``
I understand. And to make matters worse, IMHO, the financial community uses terminology that is misleading or confusing, even to a native English speaker.
That is why a concrete example of the actual calculations that you want to accomplish would be helpful.
I will try to keep my English as simple as possible. But my English is not so good either, being a born American (wink). So feel free to ask for clarification, as needed.
-----
Re: ``Correct me if I'm wrong, but if I want to use your provided formula - I need to extract the dates for deposits?``
Yes. The purpose of the TWRR is to reflect the true market rate of return, excluding "external factors" like deposits and withdrawals.
For example, if the ending balance was 100,000 yesterday, and the ending balance is 110,000 today because the market rate of return was 1% (1000) and we deposited 9000, we want the TWRR to be 1% (101000/100000 - 1), not 10% (110000/100000 - 1).
Suppose 6 days later, the ending balance is 120,000 because the market rate of return over that period was again 1% (1100) and we deposited 8900 on the last day. Again, we want the TWRR for that period to be 1% (111100/110000 - 1), not 9.09% (120000/110000 - 1).
And the cumulative market rate of return and TWRR for the total of 7 days is (1+1%)*(1+1%) - 1 = 2.01%, not 120000/100000 - 1 = 20%.
With that in mind, see the attached Excel file.
The TWRR in column E is the __cumulative__ market rate of return.
As a proof of concept, see the periodic market rate of return and the cumulative market rate of return that are calculated in columns G and H.
-----
If the cumulative period is a year or less, investment firms report the cumulative TWRR.
But if the cumulative period is more than a year, investment firms report the average compounded annual TWRR, which might be calculated by (1+cumTWRR)^(days/365) - 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 30 2021 09:40 AM
Thank you for another thorough reply and guidance.
I can only apologise for not being clear enough, but the formulas in your example was exactly what I was looking for! Thank you very much! I really liked your expanding sumproduct, haven't considered one could produce a formula like that, very neat indeed. Today I learned.. :D
I think I'll need to read through your explanation a few more times before fully comprehending it, but very useful indeed!
Colour me impressed! Thank you again!
/Q
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 30 2021 01:03 PM - edited Jul 30 2021 01:14 PM
@QWeelon wrote: ``Colour me impressed! Thank you again!``
Another child of the 1960s? (wink)
You're welcome. But I should have explained that we select the single cell E4 and array-enter the formula by pressing ctrl+shift+Enter, then copy E4 down the column.
Do not select the column of cells (E4:E33) and array-enter the formula. That does not work. But even if it did, it would be unnecessary.
(BTW, I use Excel 2010. I'm not sure you need to explicitly array-enter formulas by pressing ctrl+shift+Enter in Excel 365 and recent versions of Excel.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 30 2021 09:38 PM
Haha, I'm actually from the 80's, I've just been raised with US TV. ;)
Yes, I've managed to get it to work, so no problem there I'd say.
Although, I do have a follow-up question. Is there a simple way to augment the formula to ignore empty rows? Would prefer to keep it general and avoid simple addition of sumproducts, if possible that is.
/Q
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 30 2021 11:02 PM
@QWeelon wrote: ``Is there a simple way to augment the formula to ignore empty rows?``
I cannot answer that without a concrete example -- ideally, an Excel file.
But I have a question for you: if you allow for empy rows in your data, why not just have rows for dates when there is a deposit or a withdrawal or both, as well as rows for the initial and final balances?
See the "min data" tab of the attached Excel file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 31 2021 02:24 AM
Sorry again for not being clear enough. I got no issues with the implementation of the formula. It works flawlessly for what I specified. Now I'm just curious if it is possible to augment it to handle gap rows, see figure below where a division with zero occurs on the last row due to the empty cells prior - the selected cell will of course be empty as well in the final revision.
/Q
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 31 2021 04:25 AM - edited Jul 31 2021 04:47 AM
@QWeelon wrote: ``the selected cell will of course be empty as well in the final revision``
If you merely want the selected cell (E7) to appear blank, I can offer some idea that might or might not be acceptable. Those solutions require formulas in all rows in column E.
See the worksheets "one blank row" and "multi blank rows" in the attached Excel file.
Use "one blank row" if there is always only one blank row between data lines.
Use "multi blank rows" if there is any number of blank rows between data lines.
But if you want the entire row to be empty (no value or formula), I cannot help you.
In either case, if you use Office 365 or the latest revision of Excel (2019?), there might be new features that can help (someone) create a soluton. I am not familiar with any of those new features.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 31 2021 07:51 AM
Real great!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Apr 02 2022 05:19 AM
@QWeelon - it is time weighted because if you change the timing of the cashflows that will have an impact on the return (given your holding period is granular enough).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Apr 03 2022 09:32 AM - edited Apr 03 2022 03:16 PM
@Kashan786 wrote: ``it is time weighted because if you change the timing of the cashflows that will have an impact on the return``
You are responding to a discussion that was resolved 9 months ago correctly and to the satisfaction of the OP. More importantly, I believe your "clarification" is incorrect.
In fact, the very point of the TWR is to eliminate the effect of external cash flows from the calculation. Therefore, it is not impacted by their timing. That is what distinguishes the TWR from the IRR.
Refer to the wikipage for "time-weighted return". The English version is at https://en.wikipedia.org/wiki/Time-weighted_return .
As for the derivation of the term "time-weighted", I believe the last sentence of the first paragraph should read:
``Mathematically, the rate of return per unit time for each sub-period is geometrically weighted by the duration of the sub-period.``
IMHO, that is a mathematical nitpick, and it is incomplete. I think it should be relegated to the later section titled ``Why is it called "time-weighted"``. But beware: I believe that some details in that later section are flawed.
I am seeking to improve that wikipage without editing it directly. But I digress.
[EDIT] I've attached Excel file that demonstrates both the straight-forward sub-period calculation and the daily-weighted calculation of TWR.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jul 29 2021 08:29 AM - edited Jul 29 2021 12:51 PM
Solution
Just to clarify.... I was not suggesting any change in your format or frequency of data. It was not clear to me what problem you wanted to solve. So my intention was only to demonstrate the TWRR calculation. I should have made that clear the first time. Sorry.
-----
Re: ``I'm aiming to find a way to calculate it basically the same way my bank does``
To that end, it would be helpful to see what the "bank" calculates, and how it is reported.
Re: ``nor is my first language English, so there may have been some lost in translation``
I understand. And to make matters worse, IMHO, the financial community uses terminology that is misleading or confusing, even to a native English speaker.
That is why a concrete example of the actual calculations that you want to accomplish would be helpful.
I will try to keep my English as simple as possible. But my English is not so good either, being a born American (wink). So feel free to ask for clarification, as needed.
-----
Re: ``Correct me if I'm wrong, but if I want to use your provided formula - I need to extract the dates for deposits?``
Yes. The purpose of the TWRR is to reflect the true market rate of return, excluding "external factors" like deposits and withdrawals.
For example, if the ending balance was 100,000 yesterday, and the ending balance is 110,000 today because the market rate of return was 1% (1000) and we deposited 9000, we want the TWRR to be 1% (101000/100000 - 1), not 10% (110000/100000 - 1).
Suppose 6 days later, the ending balance is 120,000 because the market rate of return over that period was again 1% (1100) and we deposited 8900 on the last day. Again, we want the TWRR for that period to be 1% (111100/110000 - 1), not 9.09% (120000/110000 - 1).
And the cumulative market rate of return and TWRR for the total of 7 days is (1+1%)*(1+1%) - 1 = 2.01%, not 120000/100000 - 1 = 20%.
With that in mind, see the attached Excel file.
The TWRR in column E is the __cumulative__ market rate of return.
As a proof of concept, see the periodic market rate of return and the cumulative market rate of return that are calculated in columns G and H.
-----
If the cumulative period is a year or less, investment firms report the cumulative TWRR.
But if the cumulative period is more than a year, investment firms report the average compounded annual TWRR, which might be calculated by (1+cumTWRR)^(days/365) - 1.