- Home
- Microsoft 365
- Excel
- Re: Technical Documentation for Excel 365 Dynamic Arrays
Technical Documentation for Excel 365 Dynamic Arrays
- Subscribe to RSS Feed
- Mark Discussion as New
- Mark Discussion as Read
- Pin this Discussion for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 21 2021 06:06 PM
I am pretty excited about the new spilling arrays, and I would like to get a better sense of what is going on under the hood. Like
- how does Excel 365 figure out what shape a result has
- what can I get away with in terms of nesting dynamic arrays within a formula
Is there some formal technical specification of the dynamic array formula evaluation rules?
I need something more than just the user documentation of specific functions to consider performance, for instance.
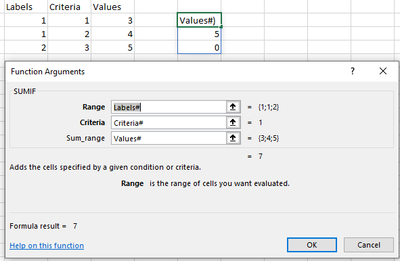
For example (see attachment) lets assume that Label#, and Values# each are single column ranges with X rows and Criteria# is a single column range with Y label values then the formula
=SUMIF(Label#,Criteria#,Values#)
will result in single column array with Y rows, thus inheriting the shape from Criteria#.
That makes total intuitive sense, but I would like to understand more systematically why and how that works. .... And, can I get fancy and and use formulas to generate Label#, Criteria# and Values#, thus nesting array formulas within the formula?
- Labels:
-
Excel
-
Formulas and Functions
-
Office 365
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 22 2021 08:22 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 22 2021 10:06 AM
@Jan Karel Pieterse thank you, this is a nice write up. I am still looking for something that goes more under the hood. Some sections of this paper go in that direction: Higher-Order Spreadsheets with Spilled Arrays - Microsoft Research. Maybe I am looking at this the wrong way and the issue isn't really the spill behavior (final stage of evaluation), but more generally how Excel decides in wich order to evaluate nested inputs, especially when some of the interim results are arrays.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 22 2021 12:31 PM
SolutionThis MS Research presentation summarises some technical aspects of array processing in Excel. To quote some of the key slides (in case the link is removed):
"1. Arrays as intermediate values
=SUM( SQRT (A1:A10) )
• De-reference the range to get a vector (= 1-D array)
• Apply SQRT to each element of the vector
• Add up the results
• SQRT has a “signature”: (Number) ->Number
2. Auto-lifting/coercion rule: when computing F(X), and the value of X is not acceptable to F (based on its signature) then
• If X is a reference, de-reference it, and try again
• If X is a string, parse it to a number and try again e.g. SQRT( “4.5” )
• If X is an array, apply F to each element of the array
3. Auto-lifting
• Works for multi-argument functions too
(*) : (Number, Number) -> Number
SUM( A1:A10 * C2:C11 )
• (*) only accepts numbers; but is given ranges
• So de-reference the ranges, and then map down the two vectors
4. The Signature Matters
INDEX : ({Matrix,Range}, Number) -> {Matrix,Range,Number,String,Boolean}
INDEX( A2:A10, {7, 3} ) returns the 2-vector {A8,A4}
• First argument of INDEX is acceptable
• Second argument is not
• So we lift only over the second"
A related thread is here: https://techcommunity.microsoft.com/t5/excel/array-formulas-array-concepts-summary-desired-and-attem...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 27 2021 02:13 AM
Picking up on your specific example of
= SUMIF(Labels#, Criteria#, Values#)Excel expects Labels# and Values# to be identically shaped arrays, but the criteria field would normally be a scalar. If it were a scalar, the function would aggregate the values to give a single value.
Because your Criteria# provides an array where a scalar is expected, Excel lifts the calculation to provide a total for each term of Criteria# individually.
With SUMIFS it is possible to have one column criteria range and another row criteria, which generates a crosstab result, rather like a pivot table.
I hope you are getting on well with the new functionality; there is a whole lot more on its way! I will most certainly never go back to the old ways of working; I would sooner dump the whole lot in the trash can and look for solutions elsewhere!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 27 2021 04:55 AM
Yes, I was lazy in copy / pasting from Microsoft material, you are right to be more specific. The function argument dialog tells us most of the info needed,
which suggests the signature is
SUMIF:( Range, {Number, String, Boolean} [, Range] ) -> NumberThis can be confirmed by checking the data types shown to the right of the input values for various test values such as 1, "1", TRUE, {1}.
In this case only scalars are shown in the Criteria argument hence the 'lifting' that occurs over the Criteria array.
It's surprising in a way that these basic evaluation mechanisms, as outlined in Simon's presentation, are not more widely known.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 27 2021 06:52 AM
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sep 22 2021 12:31 PM
SolutionThis MS Research presentation summarises some technical aspects of array processing in Excel. To quote some of the key slides (in case the link is removed):
"1. Arrays as intermediate values
=SUM( SQRT (A1:A10) )
• De-reference the range to get a vector (= 1-D array)
• Apply SQRT to each element of the vector
• Add up the results
• SQRT has a “signature”: (Number) ->Number
2. Auto-lifting/coercion rule: when computing F(X), and the value of X is not acceptable to F (based on its signature) then
• If X is a reference, de-reference it, and try again
• If X is a string, parse it to a number and try again e.g. SQRT( “4.5” )
• If X is an array, apply F to each element of the array
3. Auto-lifting
• Works for multi-argument functions too
(*) : (Number, Number) -> Number
SUM( A1:A10 * C2:C11 )
• (*) only accepts numbers; but is given ranges
• So de-reference the ranges, and then map down the two vectors
4. The Signature Matters
INDEX : ({Matrix,Range}, Number) -> {Matrix,Range,Number,String,Boolean}
INDEX( A2:A10, {7, 3} ) returns the 2-vector {A8,A4}
• First argument of INDEX is acceptable
• Second argument is not
• So we lift only over the second"
A related thread is here: https://techcommunity.microsoft.com/t5/excel/array-formulas-array-concepts-summary-desired-and-attem...