I need a formula to calculate a loan payment with additional principle added to accelerate payoff...

[Douglas997t]

Hello All!

This relates to a Mortgage Payment scenario. Calculation of the payment ( PMT(Int/12,Term,-Bal.) ) then illustrating the effects of an additional dollar amount being applied to the principle only on a monthly basis to accelerate the payoff term. I have built entire spreadsheets to accomplish this and they work beautifully. In this case I need a one formula in one cell solution to accomplish this as it will need to be available to hundreds, maybe thousands of rows each with its own specific criteria under which this calculation will need to be applied. I have included an attachment of a sample of the more spread out version of the calculation with the cheat of using my HP 17BII+ to calculate the right answer. The additional payment made each month is to be applied directly to principle as opposed to as a prepayment applied to both principle & interest.

I really appreciate your collective assistance with this one!

Douglas

[#2]

@Douglas997t  wrote:  ``The solution would need to be a single cell``

See ERRATA in subsequent two responses.

I'm confused.  Can you tell me exactly the cell references of the multiple formulas that you want to combine, and exactly the cell reference where the single formula would go?

Frankly, I like what you did in B10:B13 as-is.  I do not see anything that must be changed.

-----

@Douglas997t  wrote:  ``additional principal payments must happen in this manner as opposed to simply making this a two step loan [....] If we began a new loan at this stage, the distribution of Principal/Interest would be skewed due the front end loading of the interest in an amortization schedule ``

That is not right.  Or I don't understand what you mean by "a two-step loan".

The reason not redo the terms of the loan after payment #169 is contractual and practical, but not mathematical.

I will explain what mean by "contractual and practical" below.  But mathematically....

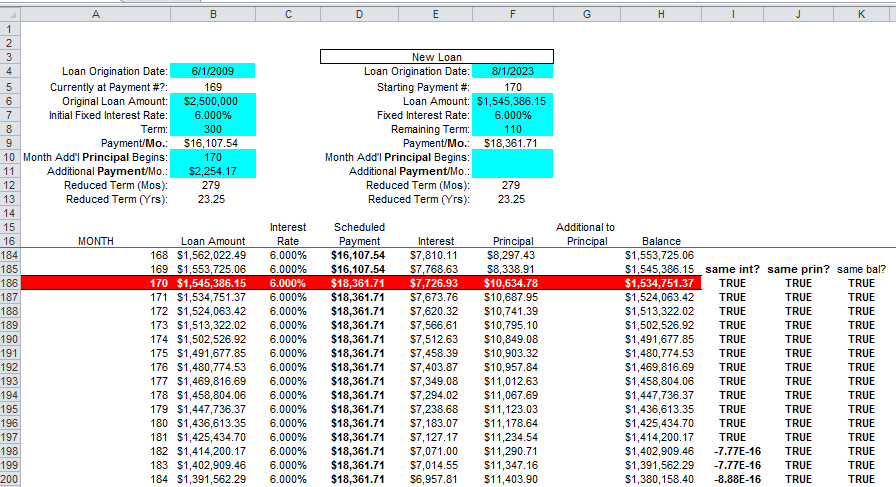
Refer to the attached Excel file, which compares your original amortization schedule (worksheet '06 - Amort Sched - Addt'l Princ') with new loan starting with payment #170 (worksheet '06 - Amort Sched - New Loan').

Note:  Freeze Pane is set after A17 in both worksheets.  Sometimes, that can be confusing.  If it is, click View > Freeze Panes > Unfreeze Panes.

Original Loan:

New Loan:

The formulas in column I, J and K demonstrate that the line-by-line interest, principal and balance are essentially the same (or relatively infinitesimally difference due to binary arithmetic anomalies).

LMK if you want me to explain any of the formulas.

-----

Re:  ``The reason not redo the terms of the loan after payment #169 is contractual and practical``

If you simply want to present the schedule of additional payments in the form of the "New Loan" worksheet, the above demonstrates that there is no harm.  Again, the mathematics are the same.

However, I agree with keeping the original loan "for real".

And to that end, I agree with presenting the additional payments as you do, even if they are consistent and equal starting with payment #170 to the (new) end.

If you restructure the loan "for real", the borrower is contractually obligated to make equal and consistent "additional payments", which are folded into the new regular payment amount.

Conversely, by retaining the original loan, the borrower has the option of not making additional payments later, or making different additional payments later.

Moreover, as a practical matter,  if you restructure the loan "for real", that is called "refinancing the loan".  Usually, the incurs "refi" loan fees that are similar to a completely new loan.

-----

Finally, a minor improvemnt....

In B5, you essentially have the expression SUM(B8)-(B8-DATEDIF(B4,TODAY(),"M")).

Algebraically, that can be reduced to just DATEDIF(B4,TODAY(),"M").

[#3]

@Douglas997t 

ERRATA....  I think I see what you mean by a "two-step loan" and changing the proportions of principal and interest per payment, as well as the issue with multiple formulas vs a single formula.

And to that end, you can consider my previous response as a "solution" that avoids all that.

In my previous response, I arbitrarily set the "new loan" payment to be the original payment plus the additional payment.

There is nothing wrong with that.  The payment can be any arbitrary that the borrower wants.

But in contrast, I suspect that you calculated the "new loan" payment by something like the following, based on the design of my "new loan" worksheet:

=ROUNDUP(PMT(F7/12,F8,-F6), 2)

where the formula in F8 is =B12-B5.

That results in a regular payment of $18,299.04, with a final payment of $18,206.92.

But the value in B12 is based on an NPER calculation that assumes a regular payment that is the same as the "arbitrary" payment that I used.

(Note the inconsistent assumptions!)

Presumably, that is the "multiple formulas" that you want to avoid.

In contrast, with the arbitrary regular payment of $18,361.71, which naturally follows from the input date in column B, namely =ROUND(B9+B11,2), the final payment is very different, namely $9154.01.

There is nothing wrong with that.  It is a consequence of the borrower's choices.

[#4]

@Douglas997t 

(Updated Excel attachment 7/4/2023 11:40 AM PT.)

ERRATA....  Sorry for the  incessant responses, but I just noticed another error in your original Excel file.

Also, I should note that in the "new loan" worksheet, the formulas starting with payment #170 are a hack -- the minimum changes to incorporate the new loan terms in F4:F13.  They are not robust enough to allow the starting payment to be anything other than #170.

As for your errors, refer to the image below.

Note that the "scheduled payment" in D295 covers only the remaining principal in B295.  It does not include the interest in E295.  It should.

And also note that the full "additional principal" payment in G295 is unnecessary.

IMHO,  the correct last "scheduled payment" in D295 should cover all of the remaining principal plus interest, even if that might exceed the regular payment in B9.

Thus, there should not be any "additional principal" payment in G295.

That is implemented by changes in the formulas starting in D17, F17 and G17.  Note that some of the changes are subtle.

The corrected image is below.  See the attached Excel file for details.

Corresponding changes are implemented in the formulas starting in C186, D186, F186 and G186 in the "new loan" worksheet.

[#5]

Hi Joe. Thanks for your guidance on this. I see what you are saying and will implement your changes! Your help is very much appreciated!

[#6]

Kudos to you for diving into the intricate world of mortgage payment calculations and extra principal payments. It's like financial wizardry, right? Your dedication to finding a streamlined solution is pretty inspiring.

Now, I get that having a one-formula solution would make life a whole lot easier, especially when dealing with heaps of rows. Speaking of navigating complex financial situations, have you ever considered connecting with a Mortgage Broker in Bridgend? They're like the pros who can help you make sense of all this and provide expert advice.

[#7]

I appreciate your kind words Roger. The solution I was shooting for would help to shortcut a number of steps and columns in an already cumbersome spreadsheet we use for commercial real estate analytics. I have created the long hand version of the net result I ultimately got to with the help of the knowledgeable and very helpful participants within this arena! Ultimately, the solution I received WAS inspired to say the least!

Thanks again for your kind words!

[#8]

@Douglas997t 

For users of 365, the solution can look very different.  For example, the outstanding loan amount would be given by

= LET(
    month,   SEQUENCE(term),
    payment, monthlyPayment + IF(month>=170, additionalPayment),
    balance, SCAN(loanAmount, payment, ClosingBalanceλ),
    loanAmt, VSTACK(loanAmount, balance),
    reduced, XMATCH(0, balance),
    TAKE(loanAmt, reduced)
  )

where

ClosingBalanceλ
= LAMBDA(priorBalance, pmt,
     MAX(priorBalance * (1 + fixedRate / 12) - pmt, 0)
  )

The other elements of the result table follow in a straightforward manner as arrays which are combined using HSTACK.

[#9]

I am a 365 user and this 2nd solution does look interesting and probably superior. But for my purpose the other solution was a bit less complicated, given that I do have some above average Excel knowledge but my skills are nowhere close to that level of complexity. Your alternative is nonetheless very much appreciated Peter!

[#10]

@Douglas997t 

I can well understand your hesitancy in committing to the new shiny toolset!  A year on and I am still refining my programming technique to take advantage of the (huge) benefits of Lambda and mitigate the remaining shortcomings.  But then, most users have developed their traditional spreadsheet techniques over a considerably greater period of time, and that supported by a myriad of posted 'tips-and-tricks'!

What I have done in the attached is move from the single measure of Loan Amount to creating the full amortisation schedule as a table [the formula being in cell B17].  Since you have 365, you may like to adjust some of your blue-shaded assumption cells to examine the manner in which the model responds.  I wouldn't trouble yourself with the 'how' of what it does, that will wait until you have the time to indulge any curiosity.

[#11]

Hey Peter. Your explanation really helps. You mentioned how some people have developed their spreadsheet techniques over many years and I would include myself in that group, at least to some degree. I began working with spreadsheets before Windows and Office had come on the scene. I started in Lotus 123 in 1986 and when DOS gave way to Win 3.1 and the 1st iteration of Excel came out, I moved to Excel and have used it every day since. My uses are somewhat rudimentary by comparison to what it is capable of and since I don't make a living from creating excel solutions for clients don't really want to go to deep within its new functionality. On the other hand, I do use it it within our practice when assessing or managing commercial real estate and love what I have been able to create using my rather old school techniques. And most importantly, I love Excel...in all of its forms! What a useful tool MS created here!

I really appreciate your help and guidance Peter. Have a great weekend!

Douglas

[#12]

the problem I have with this is that I was trying to figure this out with formulas that could add an additional payment here and there and actually see the difference

[#13]

I mean you could of just used the arrows to subtract the extra decimal places and it would of rounded it up lol but great job

[#14]

@AlThePal-78  wrote:  ``the problem I have with this is [....]``

Your comment lacks context.  I don't know what "this" is.

Also, this thread is nearly 2 years old, and it takes makes many twists and turns that might be irrelevant to your problem.

If you need help with something, I suggest that you start a new thread with a clear explanation of the problem you are having.

Attach an Excel file that demonstrates the problem (or if you cannot, post a URL to a file that you upload to a file-sharing website like box.net/files, dropbox.com, onedrive.live.com, etc.  (But not Google Sheets.)

If you wish, refer back to whatever part of this thread that is relevant.  But I suspect a new beginning will be sufficient.

[#15]

@AlThePal-78  wrote:  ``you could of just used the arrows to subtract the extra decimal places and it would of rounded it up``

One of the problems with commenting on a thread that is nearly 2 years old, especially without context, is that memories lapse.  Sometimes I cannot remember what I was talking about 2 days ago, much less 2 years.  LOL.

I'm not sure what comments about rounding (up?) you are referring to.

But if "[use] the arrows to subtract the extra decimal places" refers to formatting options (whether on the toolbar or not), I have a couple cautionary comments that might be relevant.  (Forgive if they are not.)

-----

First, changing the format to reduce the number of decimal places that are displayed results in rounding, not necessarily rounding up, the displayed value.

Sometimes, rounding looks like rounding up because, by coincidence, the digits to the right are 5... or more.  For example, formatting 1234.56 to display zero decimal places does appear to round up to 1235.  But 1234.45 will appear to round down to 1234.

If you referring to my comments about rounding up NPER and PMT results, my intention is to always round up; for instance, resulting in 1235 even in the latter example.

-----

Second and more importantly, changing the format alters only the appearance, not the actual value.  (Unless you set "Precision as displayed", which I usually do not recommend.)

In my examples above, the values remain 1234.56 and 1234.45, even if they appear to be 1235 and 1234 respsectively.  Consequently, changing their format has no impact on dependent calculations.

Again, if you are referring to my comments about rounding up NPER and PMT, my intention is to change the actual values, not merely their appearance.  IOW, I intend for the change to affect dependent calculations.